A2SB: Audio-to-Audio Schrodinger Bridges
Published:
Paper Code & Model Checkpoints (coming soon)
Author: Zhifeng Kong *, Kevin J Shih *, Weili Nie, Arash Vahdat, Sang-gil Lee, Joao Felipe Santos, Ante Jukic, Rafael Valle, Bryan Catanzaro
Posted: Zhifeng Kong
Overview
Real-world audio is often degraded by factors such as recording devices, compression, and online transfer. For instance, certain recording devices and compression methods can result in a low sampling rate, while online transfers can lead to missing audio segments. These problems are usually ill-posed and solved with data-driven generative models.
While there are many existing works for speech enhancement at around 16-24kHz, high-res music restoration at high sampling rate (44.1kHz) is a more challenging task and less studied. Our proposed A2SB model can restore music that is lowpassed or has missing segments. Compared to existing approaches, A2SB has the following advantages:
- A2SB has significantly better generation quality.
- A2SB is trained on large scale permissively-licensed music datasets.
- A2SB is an end-to-end model requiring no vocoder, making it easier to deploy.
- A2SB can support multiple tasks (bandwidth extension and inpainting) with a single model.
- A2SB can restore hour-long audio without boundary artifacts.
Samples for Bandwidth Extension
Below we demonstrate A2SB can extend lowpassed samples with a cutoff frequency at 4kHz (i.e. 8kHz sampling rate) to 22.05kHz (i.e. 44.1kHz sampling rate). A2SB has the best genration quality, is the most faithful to the inputs, and has the least hallucination.
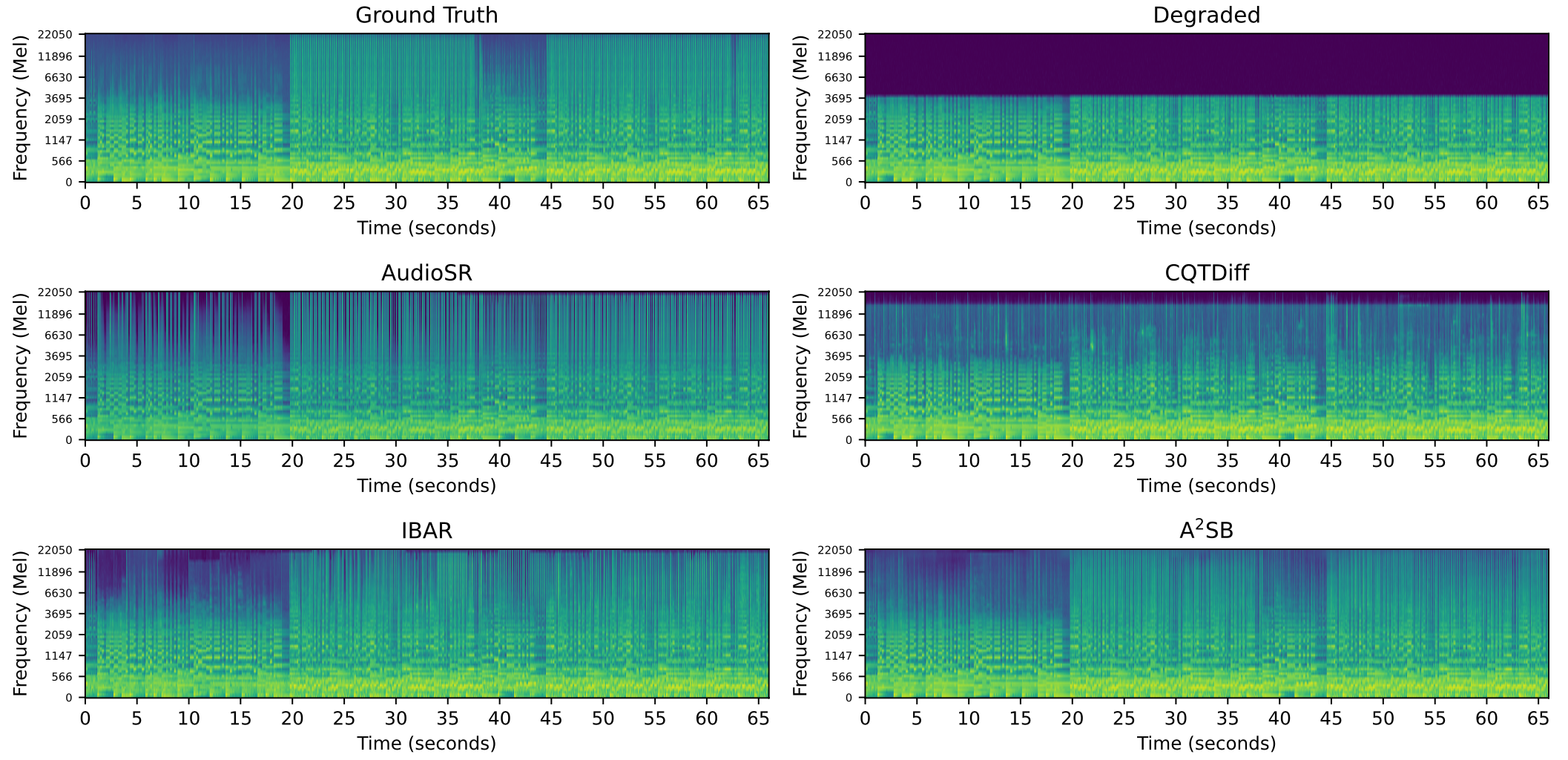
| Ground-Truth | Degraded | CQTDiff |
|---|---|---|
| AudioSR | IBAR | A2SB (ours) |
|---|---|---|
Samples for Inpainting
Below we demonstrate A2SB can inpaint missing segments of length 1000ms. There is one missing segment every 5 seconds; the missing segments are 2-3, 7-8, 12-13, 17-18, and so on. A2SB fills the missing segments the most smoothly and naturally.
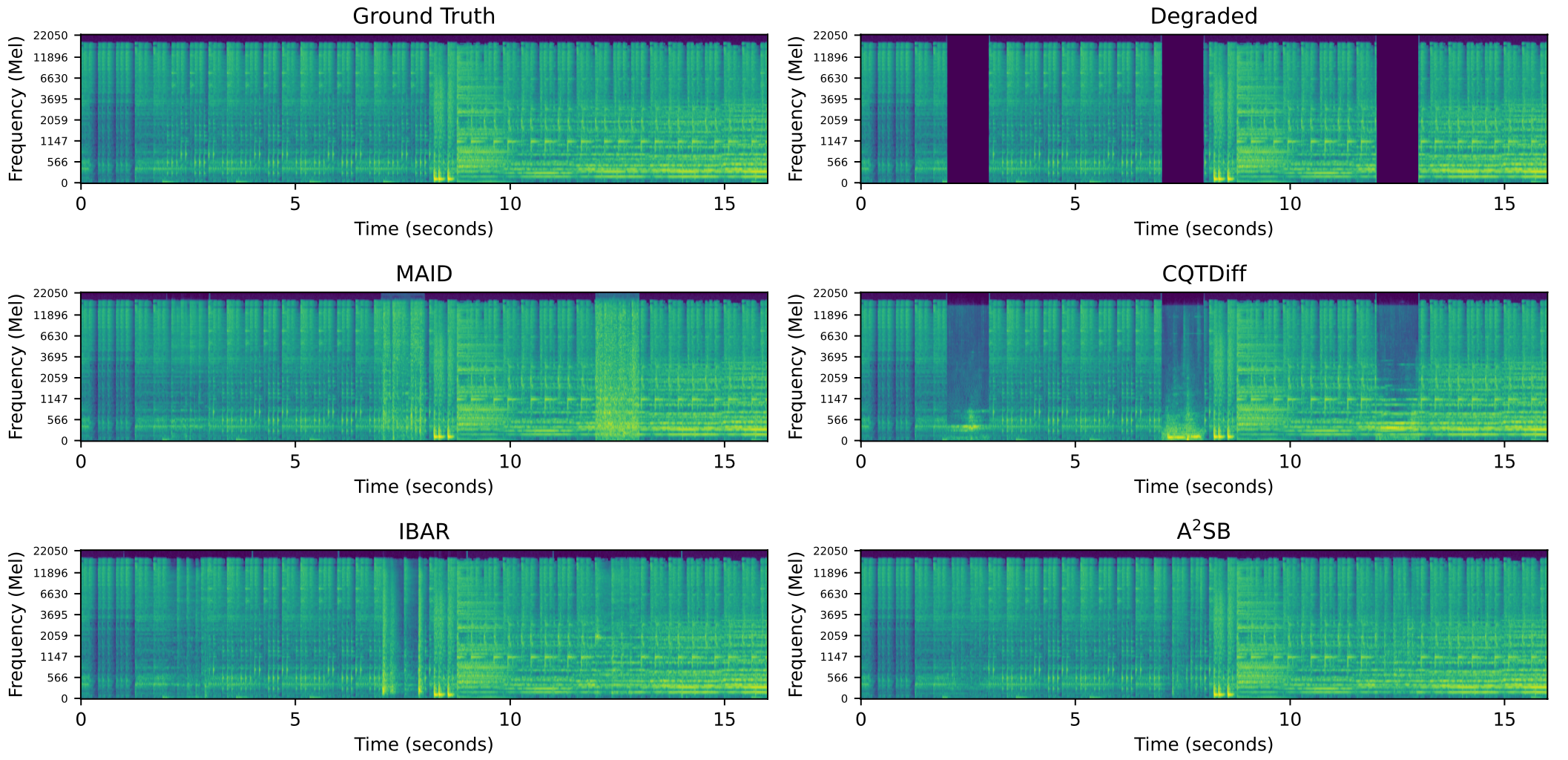
| Ground-Truth | Degraded | CQTDiff |
|---|---|---|
| MAID | IBAR | A2SB (ours) |
|---|---|---|
Factorized Audio Representation
A2SB is an end-to-end restoration model for waveform at 44.1kHz. In other words, we do not need a separate vocoder to generate waveform like most prior methods. To achieve this goal, we train our model on a factorized audio representation based on the STFT representation $(\Lambda,\Theta)$, where $\Lambda$ is the magnitude and $\Theta$ is the phase. Our factorized representation consists of three channels:
- The first channel is the power compressed magnitude $\Lambda^{\rho}$, where $\rho=0.25$ for squashing the numerical range of $\Lambda$.
- The second and third channels are the trigonometric representation of the phase: $\cos(\Theta)$ and $\sin(\Theta)$. We find these representations stabilize training more effectively and lead to better generation quality.
To invert model outputs back to waveform, we compute \(\hat{S}=\left[\begin{array}{l}\cos(\Theta)\odot (\Lambda^{\rho})^{1/\rho}\\\sin(\Theta)\odot (\Lambda^{\rho})^{1/\rho}\end{array}\right]\) Since the predicted trigonometric representations may not rigorously satisfy that the sum of squares equals to 1, we apply the SVD orthogonalization to project model outputs to proper trigonometric representations. We find the model can learn trigonometric representations pretty well and the SVD orthogonalization just does minor corrections occasionally.
Model, Architecture, and Training
A2SB is a Schrodinger Bridge model which directly transforms between a source distribution and a target distribution. Schrodinger Bridges are especially suitable for restoration tasks: when the degraded sample is partially aligned with the original sample, the source and target distributions are close.
Our loss function is \(\mathbb{E}~\left\|\mathbb{M}\odot \left(\epsilon(x_t,t)-\frac{X_t-X_0}{\sigma_t}\right)\right\|_2^2\) where $\mathbb{M}$ is the Boolean mask for bandwidth extension and inpainting tasks, $X_0$ is the clean data, $X_t$ is a linear interpolation between the clean and degraded sample, and the network $\epsilon$ is to predict $X_t-X_0$ up to a scaling factor $1/\sigma_t$ as in the Schrodinger Bridge theory.
A2SB uses an improved UNet architecture with RoPE positional embedding and an additional conditioning variable indicating the frequency bins. The network has 565M parameters.
We train A2SB in two stages.
- In the first pre-training stage, we train A2SB on 2.3K hours of music data and use bf16 for accelerated training.
- In the second fine-tuning stage, we train A2SB on a high-quality subset of 1.5K hours data. We train separate models on different $t$ (diffusion step) intervals (e.g. $(0,0.5]$ and $[0.5,1]$) for better quality.
Restore Long Audio Inputs
A2SB is trained on about 2.97 seconds of audio. However, we often want to restore longer audio in real applications. Simply concatenating restored segments can create boundary artifacts, particularly in bandwidth extension. To enable long audio restoration, we adapt the MultiDiffusion method (an inference-time panorama generation method in for vision models) to create a panorama generation of restored audio that is smooth across time. This allows us to restore very long audio inputs, e.g., an hour.
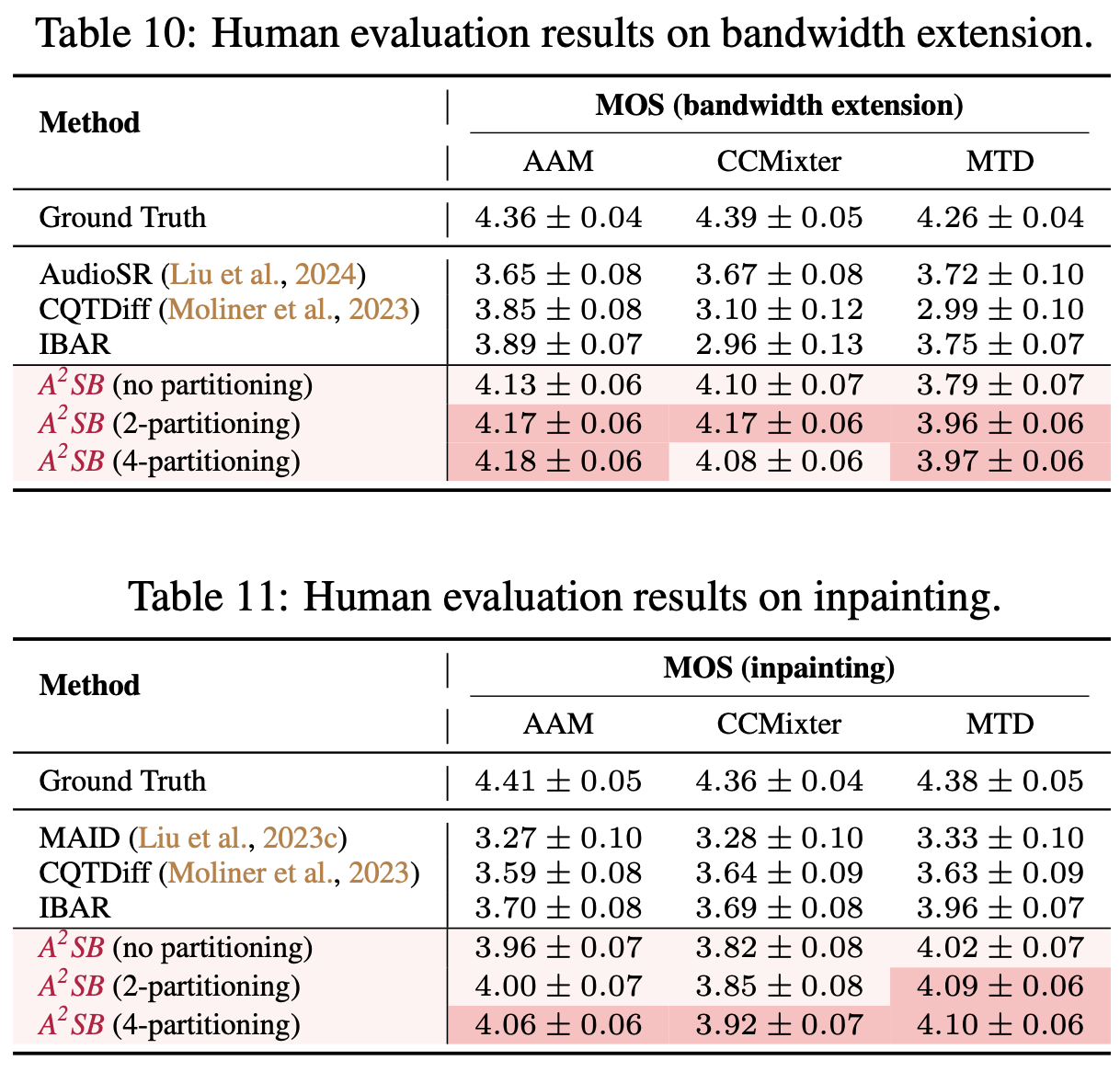
Benchmark Results
A2SB achieves the state-of-the-art bandwidth and inpainting results on objective and human evaluations. The tables below summarize the human evaluation results of A2SB.
Future Work
- We plan to extend A2SB to support more audio restoration tasks beyond bandwidth extension and inpainting
- We will investigate using the most recent advances in architectural design and large-scale training to scale-up our model to billion size for better quality, generalization, and emergent abilities.
- We will investigate better usage of training data in the setup where we combine data from very different data sources (distributions).
- We will also investigate methods for better restoration for stereo data as this is an important feature of high-quality music.
@article{kong2025a2sb,
title={A2SB: Audio-to-Audio Schr{\"o}dinger Bridges},
author={Kong, Zhifeng and Shih, Kevin J and Nie, Weili and Vahdat, Arash and Lee, Sang-gil and Santos, Joao Felipe and Juki{\'c}, Ante and Valle, Rafael and Catanzaro, Bryan},
year={2025},
journal={arXiv preprint arXiv:2025.11311},
url={https://arxiv.org/abs/2501.11311},
}
