Training Math Reasoning Model with Reinforcement Learning
Published:
AceMath-RL-Nemotron
AceMath-RL-Nemotron-8B: [Checkpoints🤗]
Author: Yang Chen, Zihan Liu, Chankyu Lee, Mohammad Shoeybi, Bryan Catanzaro, Wei Ping
Overview
We are excited to introduce AceMath-RL-Nemotron-7B, a math model trained purely with reinforcement learning (RL) from the Deepseek-R1-Distilled-Qwen-7B checkpoint. It achieves 69.0% Pass@1 accuracy on AIME 2024 (+12.5% gain from DeepSeek-R1-Distill), surpassing o3-mini (low) at 60% and o1-mini at 63.6%. On AIME 2025, it achieves 53.6% Pass@1 accuracy (+13% gain). Surprisingly, math-focused RL training also improves the model’s coding accuracy on LiveCodeBench, reaching 44.4% Pass@1 (+6.8% gain), demonstrating the generalization capabilities of scaled RL training.
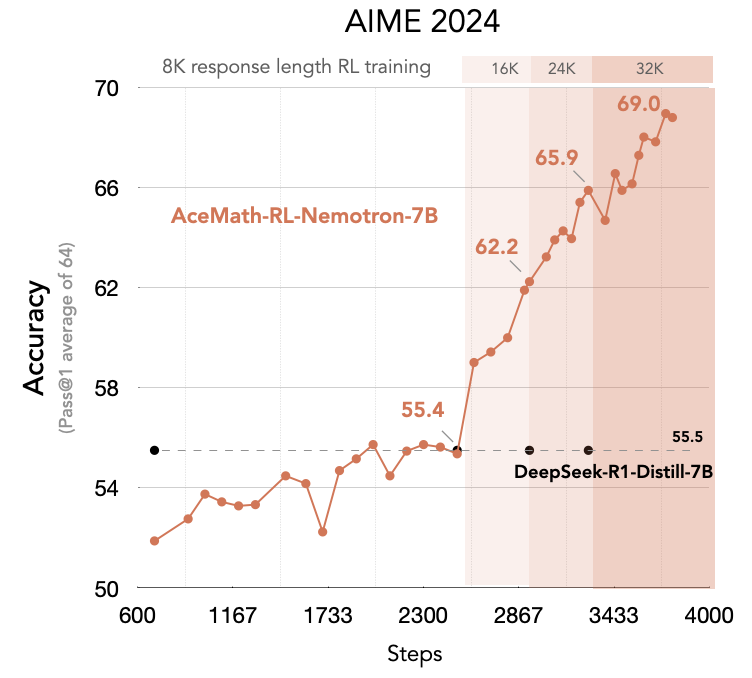
Main Takeways:
-
We find that using on-policy GRPO training is critical to preventing entropy collapse during training while ensuring sufficient exploration.
-
Curriculum learning: Response length extension training from 8K —> 16K —> 24K —> 32K
- Stage 1 (8K): reset the long CoT of the model
- Stage 2 (16K): model response length and accuracy shot up in this stage
- Stage 3 (24K) and Stage 4 (32K): use 2K difficult data based on model pass rate to boost accuracy
Main Results:
We evaluate our model against competitive reasoning models of comparable size on AIME 2024, AIME 2025, and GPQA.
| Model | AIME 2024 (AVG@64) |
AIME 2025 (AVG@64) |
GPQA-Diamond (AVG@8) |
|---|---|---|---|
| DeepSeek-R1-Distill-Qwen-7B | 55.5 | 39.2 | 49.1 |
| Light-R1-7B-DS | 59.1 | 44.3 | 49.4 |
| AReaL-boba-RL-7B | 61.9 | 48.3 | 47.6 |
| Llama-Nemotron-Nano-v1 (8B) | 63.8 | 47.1 | 54.1 |
| Skywork-OR1-Math-7B-Preview | 69.8 | 52.3 | - |
| AceMath-RL-Nemotron-7B 🤗 | 69.0 | 53.6 | 52.1 |
Additionally, we evaluate our models on additional math benchmarks and LiveCodeBench for a more comprehensive evaluation.
| Model | GSM8K (AVG@1) |
MATH500 (AVG@4) |
Minerva Math (AVG@1) |
GaoKao2023En (AVG@1) |
Olympiad Bench (AVG@1) |
College Math (AVG@1) |
ACM23 (AVG@5) |
LiveCodeBench (AVG@8) |
|---|---|---|---|---|---|---|---|---|
| DeepSeek-R1-Distill-Qwen-7B | 92.7 | 92.8 | 57.4 | 82.3 | 58.2 | 56.7 | 89.0 | 37.6 |
| AceMath-RL-Nemotron-7B 🤗 | 93.3 | 94.1 | 56.6 | 85.5 | 66.7 | 59.8 | 94.0 | 44.4 |
Training Recipe:
GRPO: on-policy training
We find that using on-policy GRPO training to be critical for preventing entropy loss collapse during training while ensuring sufficient exploration. Off-policy experiments showed entropy collapse after 150 steps, along with exploding KL loss. Despite implementing the Clip-Higher technique, these issues persisted in our experiments. Therefore, we opted to update the model parameters only once after the samples are generated from the current policy (i.e., training_batch_size == ppo_mini_batch_size in veRL).
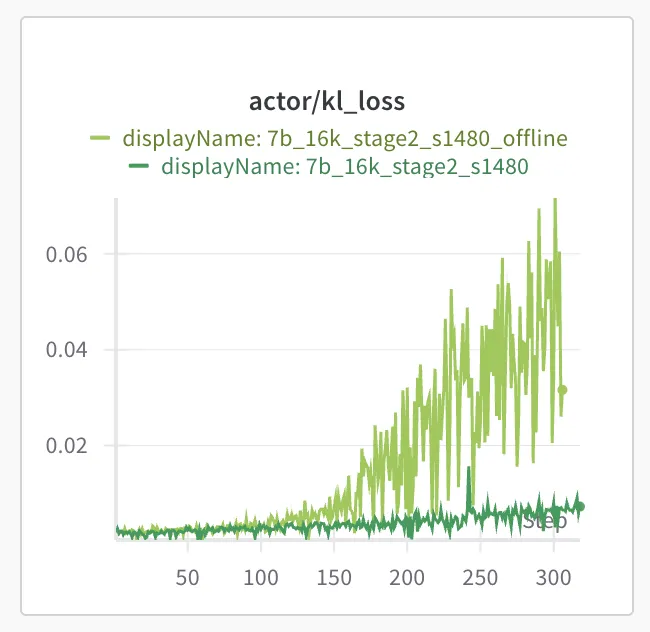
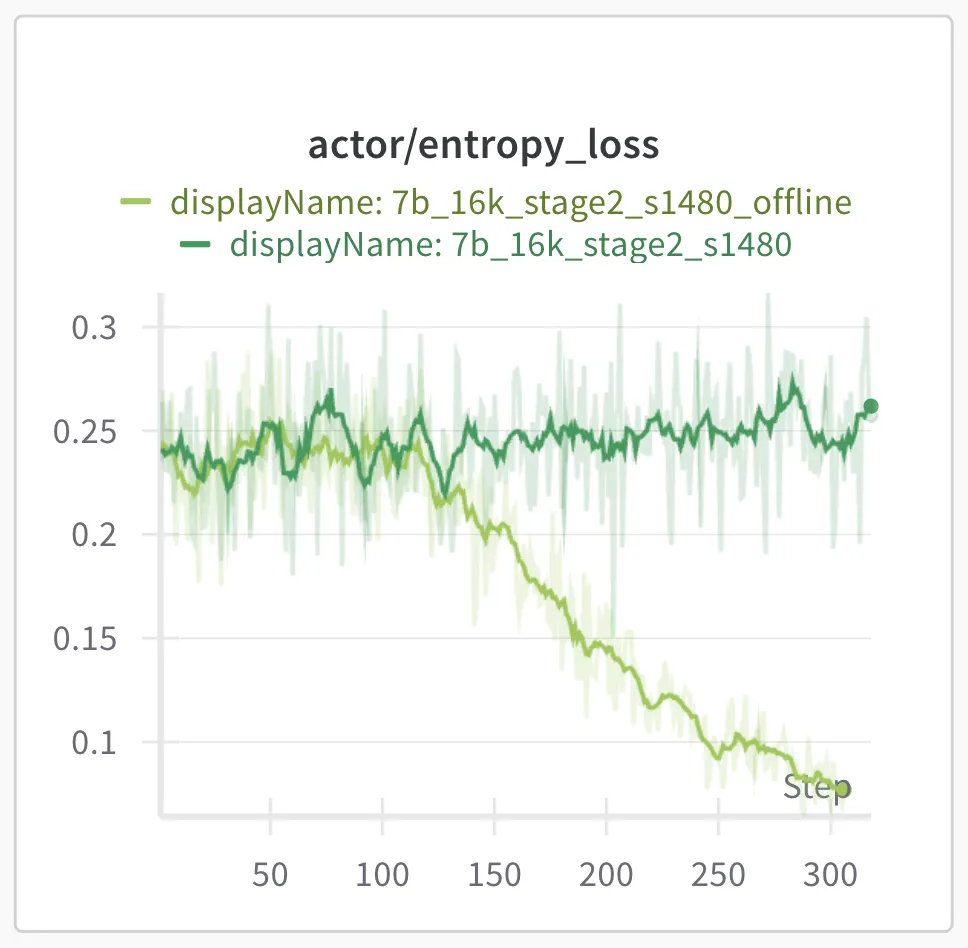
Response length extension training
| Model | AIME 2024 (avg@64) |
AIME 2025 (avg@64) |
MATH500 (avg@4) |
GPQA (avg@4) |
LiveCodeBench (avg@8) |
|---|---|---|---|---|---|
| Deepseek-R1-Distill-Qwen-7B | 55.5 | 39.01 | 92.8 | 49.1 | 37.6 |
| Stage 1 (8K) - 2500 steps | 55.36 | 42.6 | 94.1 | 51.14 | 41.89 |
| Stage 2 (16K) - 430 steps | 62.24 | 50.15 | 94.15 | 51.95 | 43.1 |
| Stage 3 (24K) - 350 steps | 65.89 | 52.5 | 94.1 | 52.15 | 44.4 |
| Stage 4 (32K) - 330 steps | 68.02 | 52.45 | 94.25 | 52.53 | 44.53 |
We follow the DeepScaler-1.5B length extension recipe to train the model across different stages. As the response length increase during each stage of training, the main computation bottleneck of the RL training lies in the sample generation. We found the length extension training strategy to be more effective and efficient compare to directly train from 16K—>24K (AIME2024 pass@1=58.9% —> 61%) with 1450 + 150 steps for each stage.
Below is the average time taken for each step for RL training with 128 H100 GPUs:
- 8K - 8 rollouts: 120s/step
- 16K - 16 rollouts: 270s/step
- 24K - 16 rollouts: 450s/step
- 32K - 16 rollouts: 580s/step
Stage 1 (8K):
In 1st stage, we train the model from 8K max response length. We observe the model response length on training set starts to drop to 3.5K first and after 450 steps starts to increase. The training set accuracy (reward/mean_accuracy) quickly improves from 65% to 80%+ after the model adapt to the 8K response length. The accuracy on AIME24 slowly improves to the initial 55% after 1,900 steps and continues to improve to 57% around 3,500 steps. We found the entropy loss to be stable around 0.25 and kl loss increase and fluctuate around 0.02 to 0.03. We didn’t observe any model collapse around training 4,000 steps.
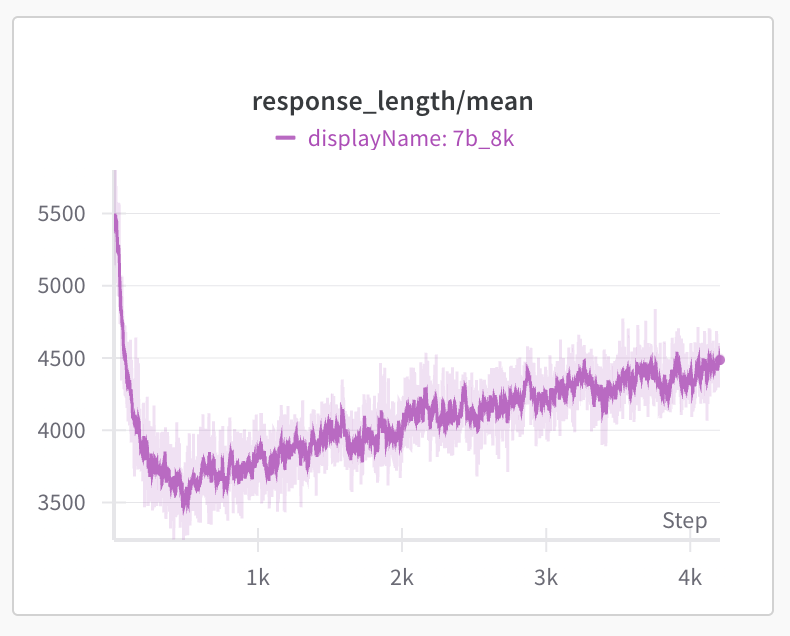
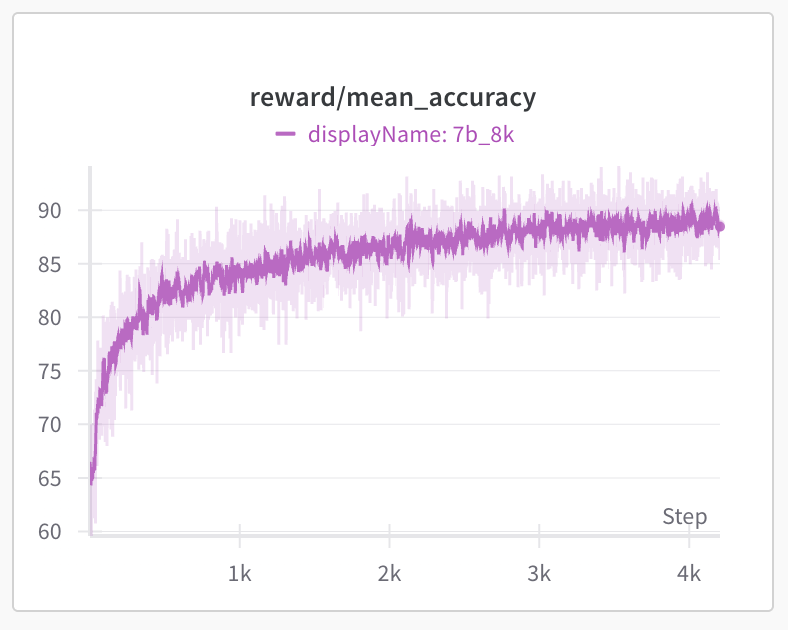
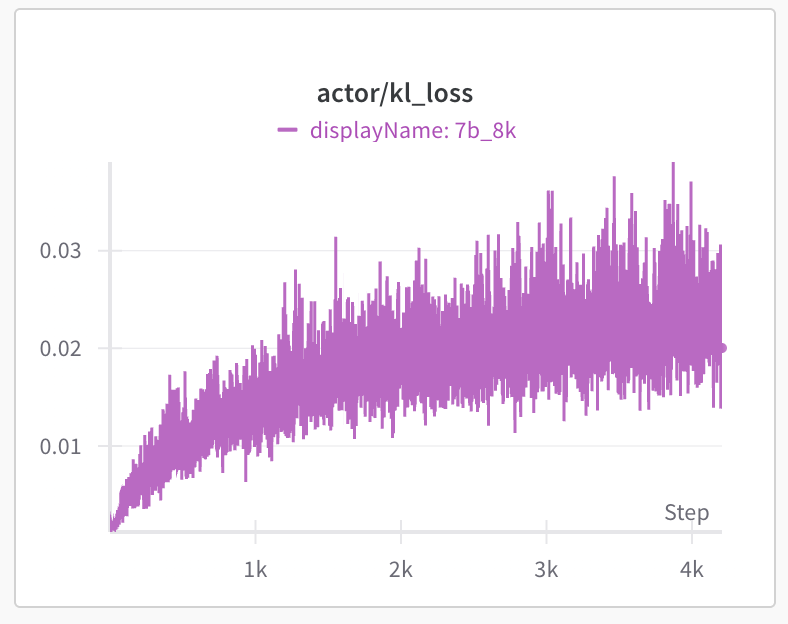
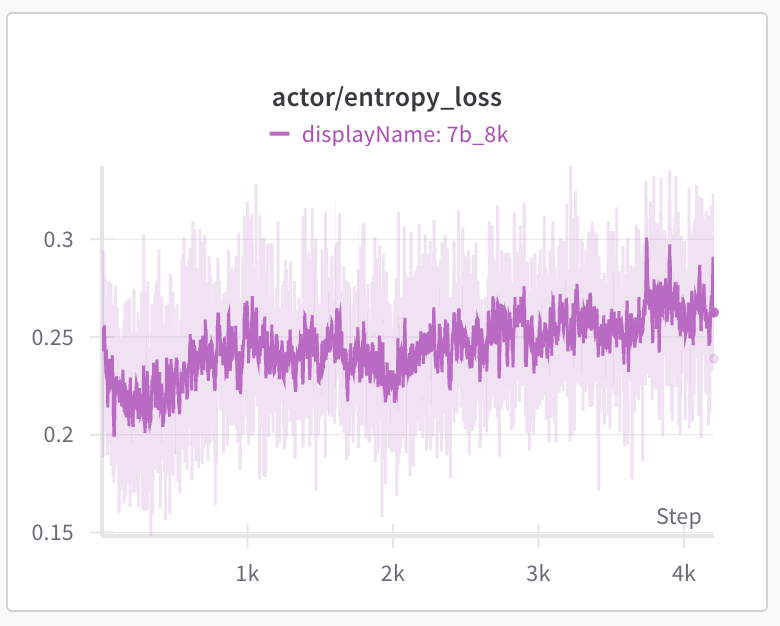
The key hyperparameters at stage 1 training are:
- temperature: 0.6
- rollout number: 8
- train batch size: 128
- kl coefficient: 0.001
Stage 2 (16K):
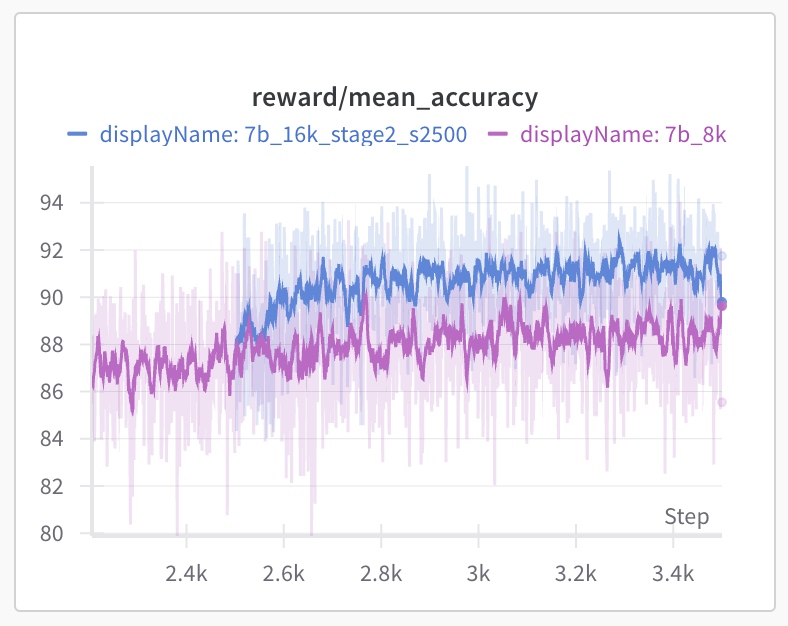
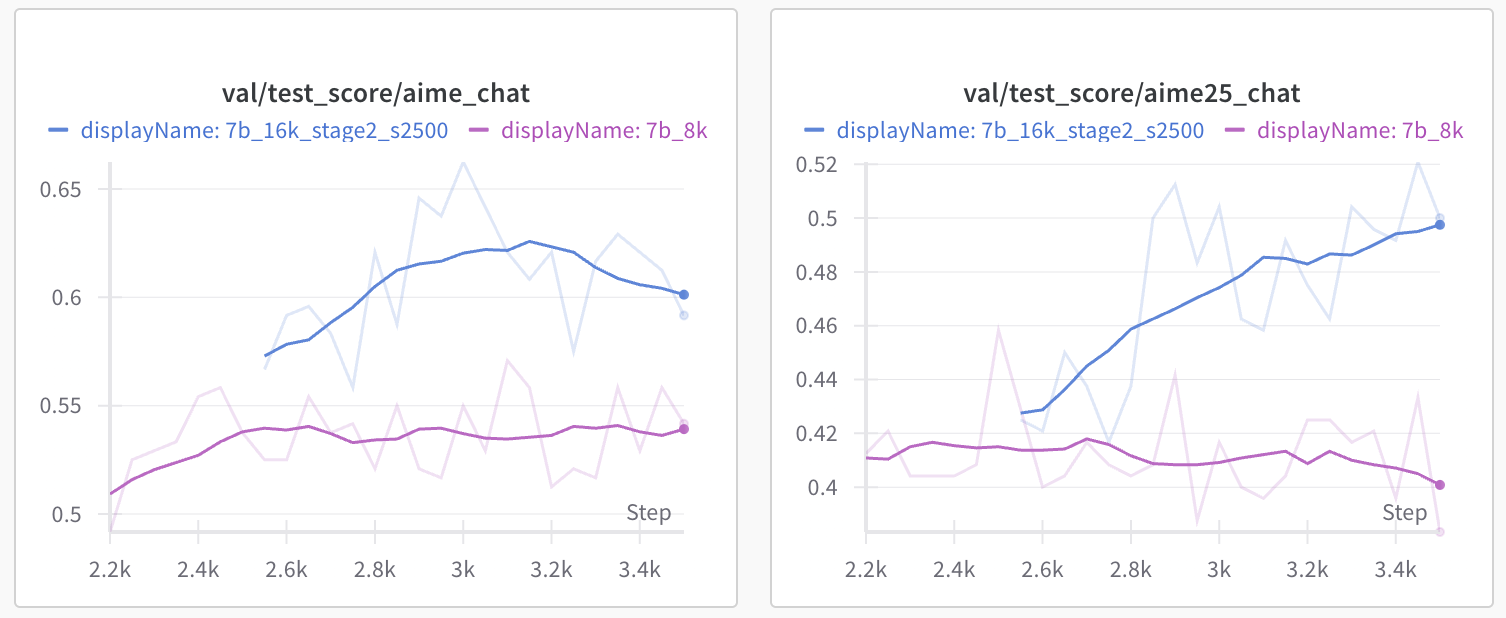
In 2nd Stage, we extend the max response length from 8K to 16K during RL training. Starting from the 2500 step checkpoint, we continue RL the model with 16K response length and increase the rollout per prompt from 8 to 16. We were excited to find that the model’s response length quickly increased from 4K to 6.5K after 400 stepsm (blue curve). Note that the purple curve corresponds to continued training with 8K max response length at stage 1. The model seem to escape from the 8K response length limit and accelerate to use more reasoning tokens. Meanwhile, the test accuracy on AIME2024 (pass@1 average 8 with 16K max response length) also jumps from 55 to 60 after few hundred steps (val/test_score/aimi_chat).
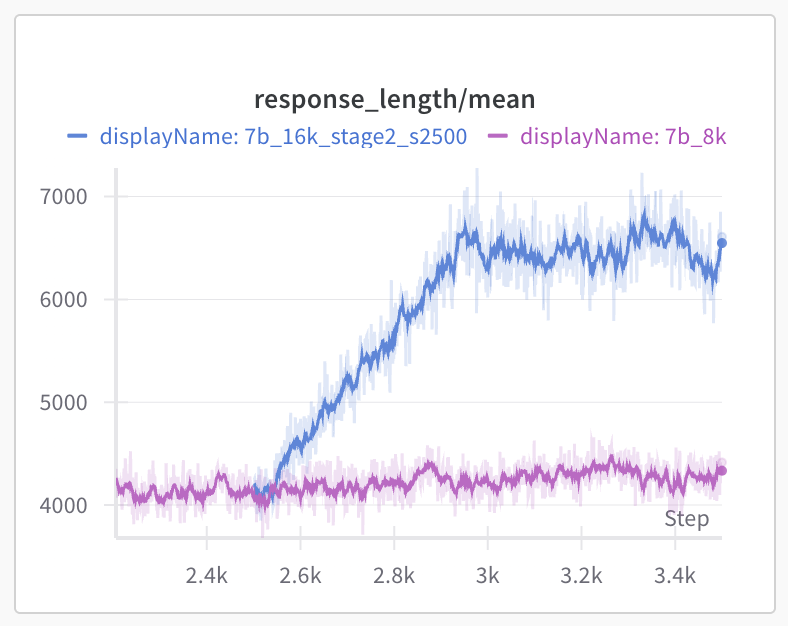
Stage 3 (24K) and 4 (32K):
During Stage 2 training, we observed that the response length on the training set reached a ceiling, fluctuating between 6K and 7K. We therefore selected the checkpoint at step 2,930 (where the response length stopped increasing) and extended the maximum response length to 24K for Stage 3 training. Additionally, with training set accuracy already around 90%+, we found that 70% of questions were achieving 100% accuracy within 16 rollouts, providing no advantage for GRPO training. As a result, we began filtering the training dataset based on the model’s pass rate. We filtered the dataset from 46K to 2.2K samples based on the model’s pass rate to focus on the most challenging problems. Our ablation study in the following Table shows that using Hard problems is most effective during stage 3 training.
| Data | AIME2024 (avg@64) |
AIME2025 (avg@64) |
|---|---|---|
| Initial Model - Stage 2 | 62.24 | 50.15 |
| Easy (#10K, pass rate ≤ 14/16) | 64.37 | 50.78 |
| Medium (#4.6K, pass rate ≤ 10/16) | 65.36 | 51.88 |
| Hard (#2.2K, pass rate ≤ 6/16) | 65.89 | 52.5 |
After Stage 3 training plateaued at around 350 steps and response lengths began to decline, we initiated a final push with 32K response length reinforcement learning. For Stage 4, we set the KL coefficient to 0. During this phase, we observed a decline in the model’s entropy loss, likely because the model is converging on the relatively small 2K training set (with only 20 steps per epoch). To encourage more exploration, we increase the temperature from 0.6 to 0.8 and 1 during training.
Citation
@article{acemath2024,
title={AceMath: Advancing Frontier Math Reasoning with Post-Training and Reward Modeling},
author={Liu, Zihan and Chen, Yang and Shoeybi, Mohammad and Catanzaro, Bryan and Ping, Wei},
journal={arXiv preprint},
year={2024}
}
