Denoising diffusion models (DDMs) have emerged as a powerful class of generative models. A forward diffusion process slowly perturbs the data, while a deep model learns to gradually denoise. Synthesis amounts to solving a differential equation (DE) defined by the learnt model. Solving the DE requires slow iterative solvers for high-quality generation. In this work, we propose Higher-Order Denoising Diffusion Solvers (GENIE): Based on truncated Taylor methods, we derive a novel higher-order solver that significantly accelerates synthesis. Our solver relies on higher-order gradients of the perturbed data distribution, that is, higher-order score functions. In practice, only Jacobian-vector products (JVPs) are required and we propose to extract them from the first-order score network via automatic differentiation. We then distill the JVPs into a separate neural network that allows us to efficiently compute the necessary higher-order terms for our novel sampler during synthesis. We only need to train a small additional head on top of the first-order score network. We validate GENIE on multiple image generation benchmarks and demonstrate that GENIE outperforms all previous solvers. Unlike recent methods that fundamentally alter the generation process in DDMs, our GENIE solves the true generative DE and still enables applications such as encoding and guided sampling.
In DDMs, a diffusion process gradually perturbs the data towards random noise, while a deep neural network learns to denoise. Formally, the problem reduces to learning the score function, i.e., the gradient of the log-density of the perturbed data. The (approximate) inverse of the forward diffusion can be described by an ordinary or a stochastic differential equation (ODE or SDE, respectively), defined by the learned score function, and can therefore be used for generation when starting from random noise.
A crucial drawback of DDMs is that the generative ODE or SDE is typically difficult to solve, due to the complex score function. Therefore, efficient and tailored samplers are required for fast synthesis. In this work, building on the generative ODE, we rigorously derive a novel second-order ODE solver using truncated Taylor methods (TTMs). These higher-order methods require higher-order gradients of the ODE—in our case this includes higher-order gradients of the log-density of the perturbed data, i.e., higher-order score functions. Because such higher-order scores are usually not available, existing works typically use simple first-order solvers or samplers with low accuracy, higher-order methods that rely on suboptimal finite difference or other approximations, or alternative approaches for accelerated sampling. Here, we fundamentally avoid such approximations and directly model the higher-order gradient terms: Importantly, our novel Higher-Order Denoising Diffusion Solver (GENIE) relies on Jacobian-vector products (JVPs) involving second-order scores. We propose to calculate these JVPs by automatic differentiation of the regular learnt first-order scores. For computational efficiency, we then distill the entire higher-order gradient of the ODE, including the JVPs, into a separate neural network. In practice, we only need to add a small head to the first-order score network to predict the components of the higher-order ODE gradient. By directly modeling the JVPs we avoid explicitly forming high-dimensional higher-order scores. Intuitively, the higher-order terms in GENIE capture the local curvature of the ODE and enable larger steps when iteratively solving the generative ODE.
The so-known DDIM solver is simply Euler's method applied to a reparameterization of the Probability Flow ODE. In this work, we apply the second TTM to this re-parameterized ODE, which results in the GENIE scheme (simplified notation; see paper for details)
\(\mathbf{x}_{t_{n+1}} = \mathbf{x}_{t_n} + h_n \mathbf{\epsilon}_\mathbf{\theta}(\mathbf{x}_{t_n}, t_n) + \frac{1}{2} h_n^2 \frac{d\mathbf{\epsilon}_\mathbf{\theta}}{dt}(\mathbf{x}_{t_n}, t_n).\)
Intuitively, the higher-order gradient term \(\frac{d\mathbf{\epsilon}_\mathbf{\theta}}{dt}\) used in GENIE models the local curvature of the ODE. This translates into a Taylor formula-based extrapolation that is quadratic in time and more accurate than linear extrapolation as in DDIM, thereby enabling larger time steps (see visualization above). We showcase the benefit of GENIE on a 2D toy distribution (see visualization below) for which we know \(\mathbf{\epsilon}_\mathbf{\theta}\) and \(\frac{d\mathbf{\epsilon}_\mathbf{\theta}}{dt}\) analytically.
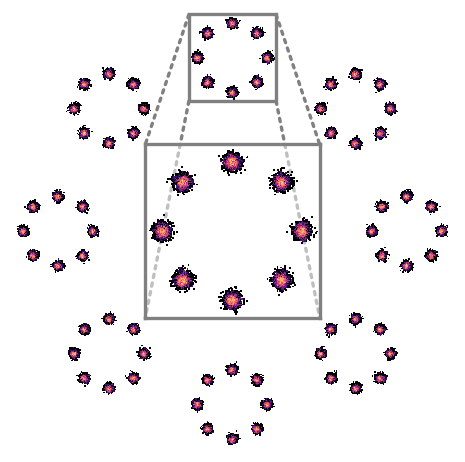
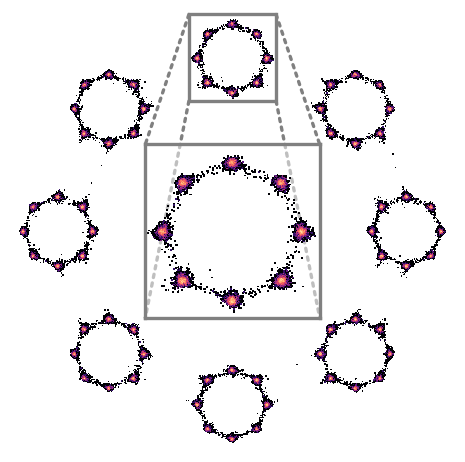
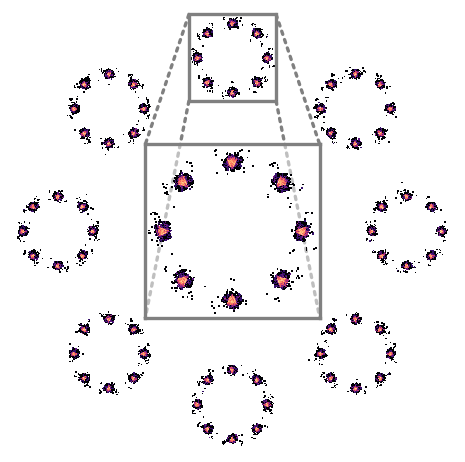
Modeling a complex 2D toy distribution: Samples in (b) and (c) are generated via DDIM and GENIE, respectively, with 25 solver steps using the analytical score function of the ground truth distribution.
Learning Higher-Order Derivatives. Regular DDMs learn a model \(\mathbf{\epsilon}_\mathbf{\theta}\) for the first-order score; however, the higher-order gradient term \(\frac{d\mathbf{\epsilon}_\mathbf{\theta}}{dt}\) required for GENIE is not immediately available to us, unlike in the toy example above. Given a DDM, that is, given \(\mathbf{\epsilon}_\mathbf{\theta}\), we could compute the higher-order derivative using automatic differentiation (AD). This would, however, make a single step of GENIE at least twice as costly as DDIM. To avoid this overhead, we propose to first distill the higher-order derivative into a separate neural network \(\mathbf{k}_\mathbf{\psi}\). We implement this neural network as a small prediction head on top of the standard DDM U-Net. During distillation training, we use the slow AD-based calculation of the higher-order derivative, but during synthesis we call the fast network \(\mathbf{k}_\mathbf{\psi}\). The model structure is visualized below.
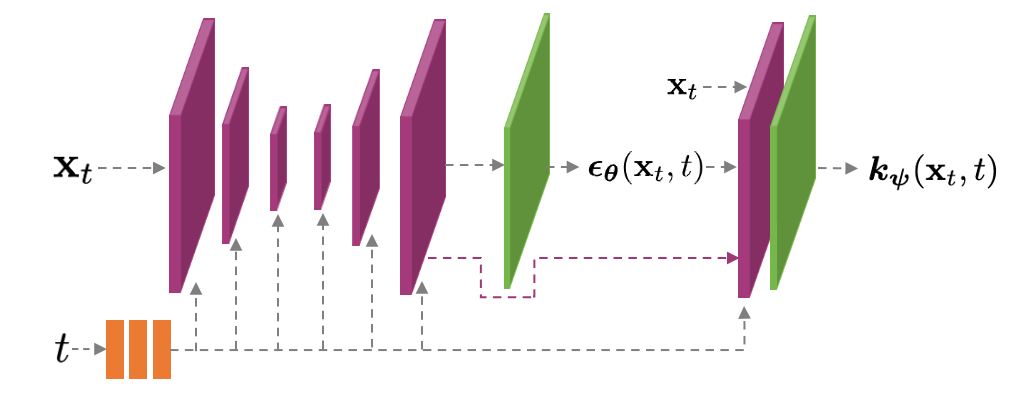
Our distilled model \(\mathbf{k}_\mathbf{\psi}\) that predicts the gradient \(\frac{d\mathbf{\epsilon}_\mathbf{\theta}}{dt}\) is implemented as a small additional output head on top of the first-order score model \(\mathbf{\epsilon}_\mathbf{\theta}.\) This model structure makes the evaluation of \(\mathbf{k}_\mathbf{\psi}\) fast when compared to \(\mathbf{\epsilon}_\mathbf{\theta}\) itself. Purple layers are used both in \(\mathbf{\epsilon}_\mathbf{\psi}\) and \(\mathbf{k}_\mathbf{\psi}\); green layers are specific for \(\mathbf{\epsilon}_\mathbf{\psi}\) and \(\mathbf{k}_\mathbf{\psi}\).
We extensively validate GENIE on several popular benchmark datasets for image synthesis, namely, CIFAR-10 (resolution \(32 \times 32\)), LSUN Bedrooms (\(128 \times 128\)), LSUN Church-Outdoor (\(128 \times 128\)), and (conditional) ImageNet (\(64 \times 64\)). We demonstrate that GENIE outperforms all previous solvers as measured by FID score for different numbers of denoising steps during generation. See paper for details.
In contrast to recent methods for accerlerated sampling of DDMs that abandon the ODE/SDE framework, GENIE can readily be combined with techniques such as classifier(-free) guidance (see examples below) and image encoding. These techniques can play an important role in synthesizing photorealistic images from DDMs, as well as for image editing tasks.
Image synthesis with classifier-free guidance for the ImageNet classes Pembroke Welsh Corgi and Streetcar using different numbers of denoising steps during generation.
We also train a high-resolution model on AFHQv2 (subset of cats only). We train a base DDM at resolution \(128 \times 128\) and a \(128 \times 128 \rightarrow 512 \times 512\) DDM-based upsampler. We are aiming to test whether GENIE also works for high-resolution image generation and in DDM-based upsamplers, which have become an important ingredient in modern large-scale DDM-based image generation systems.
High-resolution images generated with the \(128 \times 128 \rightarrow 512 \times 512\) GENIE upsampler using only five function evaluations. For the two images at the top, the upsampler is
conditioned on test images from the Cats dataset. For the two images at the bottom, the upsampler is conditioned on samples from the \(128 \times 128\) GENIE base model (using 25 function evaluations);
an upsampler evaluation is roughly four times as expensive as a base model evaluation.
The sequence above is generated by randomly traversing the latent space of our GENIE model (using 25 base model and five upsampler evaluations). We are interpolating in the latent space of the base model, and we keep the noise in the upsampler (both latent space and augmentation perturbations) fixed in all frames.
GENIE: Higher-Order Denoising Diffusion Solvers Tim Dockhorn, Arash Vahdat, Karsten Kreis Advances in Neural Information Processing Systems, 2022Experimental Results



Paper
@inproceedings{dockhorn2022genie,
title={{{GENIE: Higher-Order Denoising Diffusion Solvers}}},
author={Dockhorn, Tim and Vahdat, Arash and Kreis, Karsten},
booktitle={Advances in Neural Information Processing Systems},
year={2022}
}