Abstract
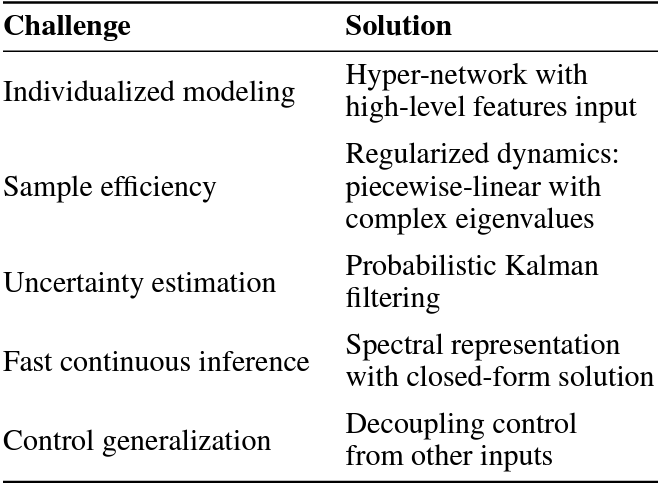
Dosing models often use differential equations to model biological dynamics. Neural differential equations in particular can learn to predict the derivative of a process, which permits predictions at irregular points of time. However, this temporal flexibility often comes with a high sensitivity to noise, whereas medical problems often present high noise and limited data. Moreover, medical dosing models must generalize reliably over individual patients and changing treatment policies. To address these challenges, we introduce the Neural Eigen Stochastic Differential Equation algorithm (NESDE). NESDE provides individualized modeling (using a hypernetwork over patient-level parameters); generalization to new treatment policies (using decoupled control); tunable expressiveness according to the noise level (using piecewise linearity); and fast, continuous, closed-form prediction (using spectral representation). We demonstrate the robustness of NESDE in both synthetic and real medical problems, and use the learned dynamics to publish simulated medical gym environments.
 |
|---|
| A summary of NESDE’s features |
Cite the paper
@InProceedings{nesde,
title = {Individualized Dosing Dynamics via Neural Eigen Decomposition},
author = {Belogolovsky, Stav and Greenberg, Ido and Eytan, Danny and Mannor, Shie},
booktitle = {Advances in Neural Information Processing Systems},
year = {2023},
publisher = {PMLR},
}