Optimization or Architecture: How to Hack Kalman Filtering

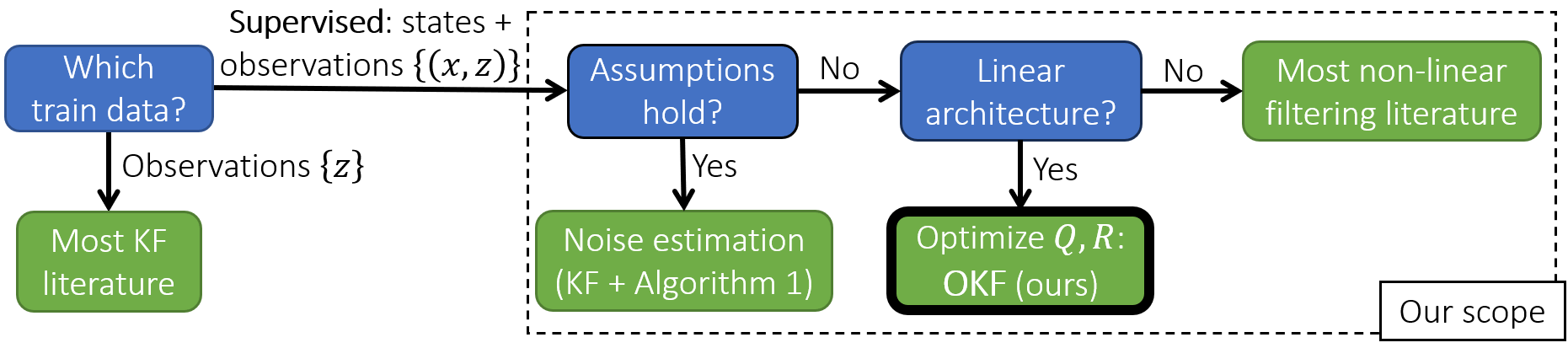
Since the KF assumptions are often violated, noise estimation is not a proxy to MSE optimization. Instead, our method (OKF) optimizes the MSE directly. In particular, neural network models should be tested against OKF rather than the non-optimized KF – in contrast to the common practice in the literature.

Code

• PyPI: pip install Optimized-Kalman-Filter
• GitHub

Abstract

In non-linear filtering, it is traditional to compare non-linear architectures such as neural networks to the standard linear Kalman Filter (KF). We observe that this mixes the evaluation of two separate components: the non-linear architecture, and the parameters optimization method. In particular, the non-linear model is often optimized, whereas the reference KF model is not. We argue that both should be optimized similarly, and to that end present the Optimized KF (OKF). We demonstrate that the KF may become competitive to neural models - if optimized using OKF. This implies that experimental conclusions of certain previous studies were derived from a flawed process. The advantage of OKF over the standard KF is further studied theoretically and empirically, in a variety of problems. Conveniently, OKF can replace the KF in real-world systems by merely updating the parameters.

Cite the paper

@InProceedings{okf,
  title = 	 {Optimization or Architecture: How to Hack Kalman Filtering},
  author =       {Greenberg, Ido and Yannay, Netanel and Mannor, Shie},
  booktitle = 	 {Advances in Neural Information Processing Systems},
  year = 	 {2023},
  publisher =    {PMLR},
}