SZ Sequences: Binary-Constructed (0, 2^q)-Sequences

Abstract

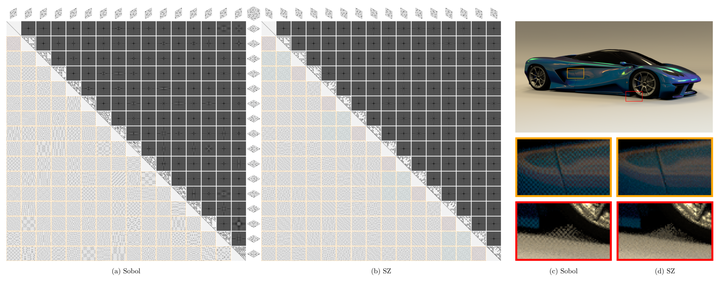
Low-discrepancy sequences have seen widespread adoption in computer graphics thanks to the superior rates of convergence that they provide. Because rendering integrals often are comprised of products of lower-dimensional integrals, recent work has focused on developing sequences that are also well-distributed in lower-dimensional projections. To this end, we introduce a novel construction of binary-based (0, 4)-sequences; that is, progressive fully multi-stratified sequences of 4D points, and extend the idea to higher power-of-two dimensions. We further show that not only it is possible to nest lower-dimensional sequences in higher-dimensional ones—for example, embedding a (0, 2)-sequence within our (0, 4)-sequence—but that we can ensemble two (0, 2)-sequences into a (0, 4)-sequence, four (0, 4)-sequences into a (0, 16)-sequence, and so on. Such sequences can provide excellent rates of convergence when integrals include lower-dimensional integration problems in 2, 4, 16,… dimensions. Our construction is based on using 2×2 block matrices as symbols to construct larger matrices that potentially generate a sequence with the target (0, s)-sequence in base s property. We describe how to search for suitable alphabets and identify two distinct, cross-related alphabets of block symbols, which we call s and z, hence SZ for the resulting family of sequences. Given the alphabets, we construct candidate generator matrices and search for valid sets of matrices. We then infer a simple recurrence formula to construct full-resolution (64-bit) matrices. Because our generator matrices are binary, they allow highly-efficient implementation using bitwise operations and can be used as a drop-in replacement for Sobol matrices in existing applications. We compare SZ sequences to state-of-the-art low discrepancy sequences, and demonstrate mean relative squared error improvements up to 1.93× in common rendering applications.