Feedforward and Recurrent Neural Networks Backward Propagation and Hessian in Matrix Form

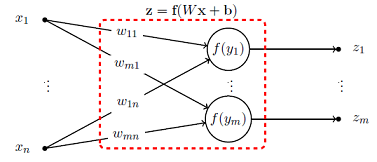
In this paper we focus on the linear algebra theory behind feedforward (FNN) and recurrent (RNN) neural networks. We review backward propagation, including backward propagation through time (BPTT). Also, we obtain a new exact expression for Hessian, which represents second order effects. We show that for t time steps the weight gradient can be expressed as a rank-t matrix, while the weight Hessian is as a sum of t2 Kronecker products of rank-1 and WTAW matrices, for some matrix A and weight matrix W. Also, we show that for a mini-batch of size r, the weight update can be expressed as a rank-rt matrix. Finally, we briefly comment on the eigenvalues of the Hessian matrix.