On the Universality of Rotation Equivariant Point Cloud Networks
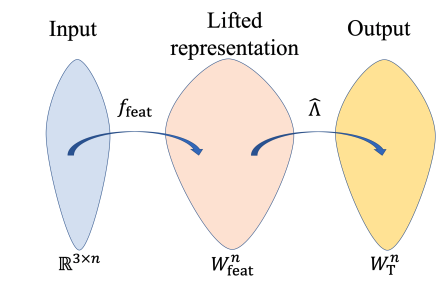
Learning functions on point clouds has applications in many fields, including computer vision, computer graphics, physics, and chemistry. Recently, there has been a growing interest in neural architectures that are invariant or equivariant to all three shape-preserving transformations of point clouds: translation, rotation, and permutation. In this paper, we present a first study of the approximation power of these architectures. We first derive two sufficient conditions for an equivariant architecture to have the universal approximation property, based on a novel characterization of the space of equivariant polynomials. We then use these conditions to show that two recently suggested models are universal, and for devising two other novel universal architectures.
