A Decomposition for In-place Array Transposition
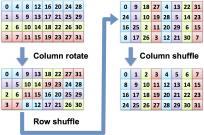
We describe a decomposition for in-place matrix transposition, with applications to Array of Structures memory accesses on SIMD processors. Traditional approaches to in-place matrix transposition involve cycle following, which is difficult to parallelize, and on matrices of dimension m by n require O(mn log mn) work when limited to less than O(mn) auxiliary space. Our decomposition allows the rows and columns to be operated on independently during in-place transposition, reducing work complexity to O(mn), given O(max(m, n)) auxiliary space. This decomposition leads to an efficient and naturally parallel algorithm: we have measured median throughput of 19.5 GB/s on an NVIDIA Tesla K20c processor. An implementation specialized for the skinny matrices that arise when converting Arrays of Structures to Structures of Arrays yields median throughput of 34.3 GB/s, and a maximum throughput of 51 GB/s. Because of the simple structure of this algorithm, it is particularly suited for implementation using SIMD instructions to transpose the small arrays that arise when SIMD processors load from or store to Arrays of Structures. Using this algorithm to cooperatively perform accesses to Arrays of Structures, we measure 180 GB/s throughput on the K20c, which is up to 45 times faster than compiler-generated Array of Structures accesses. In this paper, we explain the algorithm, prove its correctness and complexity, and explain how it can be instantiated efficiently for solving various transpose problems on both CPUs and GPUs.
Publication Date
Published in
Research Area
Uploaded Files
Copyright
Copyright by the Association for Computing Machinery, Inc. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from Publications Dept, ACM Inc., fax +1 (212) 869-0481, or permissions@acm.org. The definitive version of this paper can be found at ACM's Digital Library http://www.acm.org/dl/.
