Fast Tridiagonal Solvers on the GPU
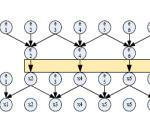
We study the performance of three parallel algorithms and their hybrid variants for solving tridiagonal linear systems on a GPU: cyclic reduction (CR), parallel cyclic reduction (PCR) and recursive doubling (RD). We develop an approach to measure, analyze, and optimize the performance of GPU programs in terms of memory access, computation, and control overhead.We find that CR enjoys linear algorithm complexity but suffers from more algorithmic steps and bank conflicts, while PCR and RD have fewer algorithmic steps but do more work each step. To combine the benefits of the basic algorithms, we propose hybrid CR+PCR and CR+RD algorithms, which improve the performance of PCR, RD and CR by 21%, 31% and 61% respectively. Our GPU solvers achieve up to a 28x speedup over a sequential LAPACK solver, and a 12x speedup over a multi-threaded CPU solver.
Publication Date
Research Area
Uploaded Files
Copyright
Copyright by the Association for Computing Machinery, Inc. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from Publications Dept, ACM Inc., fax +1 (212) 869-0481, or permissions@acm.org. The definitive version of this paper can be found at ACM's Digital Library http://www.acm.org/dl/.
