Parallel Solution of Sparse Triangular Linear Systems in the Preconditioned Iterative Methods on the GPU

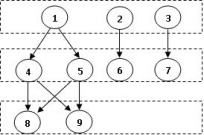
A novel algorithm for solving in parallel a sparse triangular linear system on a graphical processing unit is proposed. It implements the solution of the triangular system in two phases. First, the analysis phase builds a dependency graph based on the matrix sparsity pattern and groups the independent rows into levels. Second, the solve phase obtains the full solution by iterating sequentially across the constructed levels. The solution elements corresponding to each single level are obtained at once in parallel. The numerical experiments are also presented and it is shown that the incomplete-LU and Cholesky preconditioned iterative methods, using the parallel sparse triangular solve algorithm, can achieve on average more than 2x speedup on graphical processing units (GPUs) over their CPU implementation.