On Learning Sets of Symmetric Elements

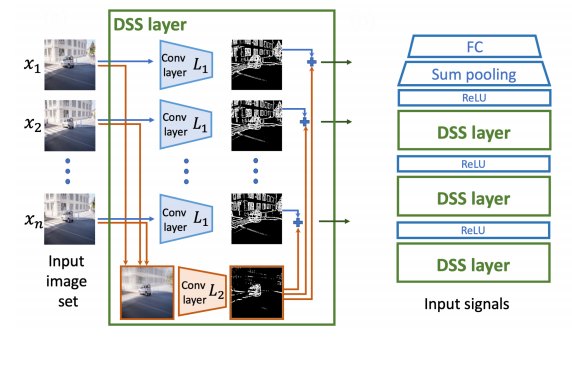
Learning from unordered sets is a fundamental learning setup, recently attracting increasing attention. Research in this area has focused on the case where elements of the set are represented by feature vectors, and far less emphasis has been given to the common case where set elements themselves adhere to their own symmetries. That case is relevant to numerous applications, from deblurring image bursts to multi-view 3D shape recognition and reconstruction. In this paper, we present a principled approach to learning sets of general symmetric elements. We first characterize the space of linear layers that are equivariant both to element reordering and to the inherent symmetries of elements, like translation in the case of images. We further show that networks that are composed of these layers, called Deep Sets for Symmetric Elements layers (DSS), are universal approximators of both invariant and equivariant functions. DSS layers are also straightforward to implement. Finally, we show that they improve over existing set-learning architectures in a series of experiments with images, graphs, and point-clouds.