Neural Control Variates
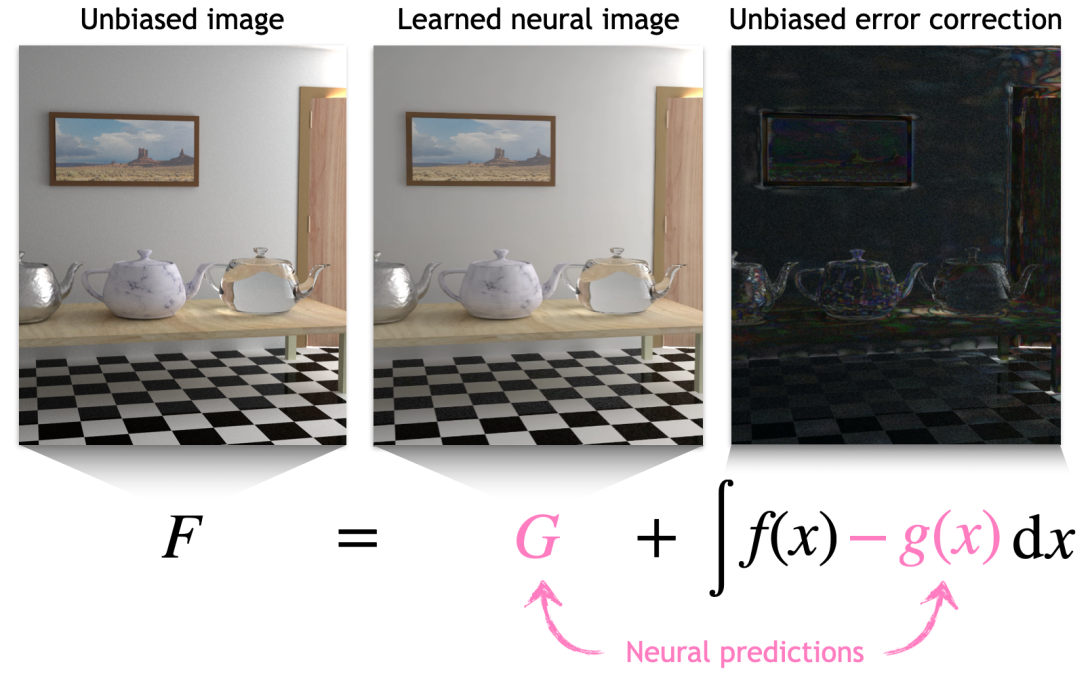
We propose neural control variates (NCV) for unbiased variance reduction in parametric Monte Carlo integration. So far, the core challenge of applying the method of control variates has been finding a good approximation of the integrand that is cheap to integrate. We show that a set of neural networks can face that challenge: a normalizing flow that approximates the shape of the integrand and another neural network that infers the solution of the integral equation. We also propose to leverage a neural importance sampler to estimate the difference between the original integrand and the learned control variate. To optimize the resulting parametric estimator, we derive a theoretically optimal, variance-minimizing loss function, and propose an alternative, composite loss for stable online training in practice. When applied to light transport simulation, neural control variates are capable of matching the state-of-the-art performance of other unbiased approaches, while providing means to develop more performant, practical solutions. Specifically, we show that the learned light-field approximation is of sufficient quality for high-order bounces, allowing us to omit the error correction and thereby dramatically reduce the noise at the cost of negligible visible bias.
Publication Date
Published in
Copyright
Copyright by the Association for Computing Machinery, Inc. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from Publications Dept, ACM Inc., fax +1 (212) 869-0481, or permissions@acm.org. The definitive version of this paper can be found at ACM's Digital Library http://www.acm.org/dl/.
