Learning the Pareto Front with Hypernetworks
Multi-objective optimization problems are prevalent in machine learning. These problems have a set of optimal solutions, called the Pareto front, where each point on the front represents a different trade-off between possibly conflicting objectives. Recent optimization algorithms can target a specific desired ray in loss space, but still face two grave limitations: (i) A separate model has to be trained for each point on the front; and (ii) The exact trade-off must be known prior to the optimization process. Here, we tackle the problem of learning the entire Pareto front, with the capability of selecting a desired operating point on the front after training. We call this new setup Pareto-Front Learning (PFL).
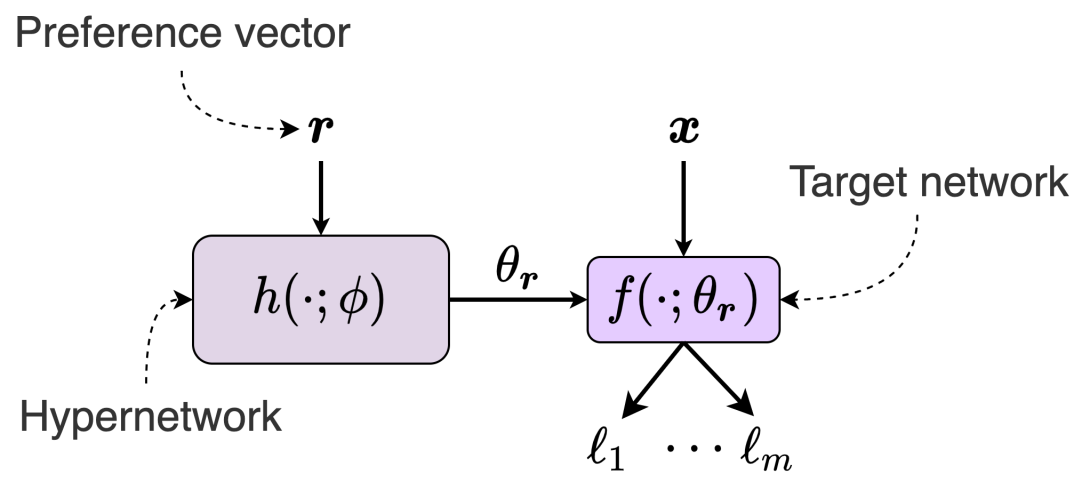
We describe an approach to PFL implemented using HyperNetworks, which we term Pareto HyperNetworks (PHNs). PHN learns the entire Pareto front simultaneously using a single hypernetwork, which receives as input a desired preference vector and returns a Pareto-optimal model whose loss vector is in the desired ray. The unified model is runtime efficient compared to training multiple models, and generalizes to new operating points not used during training. We evaluate our method on a wide set of problems, from multi-task regression and classification to fairness. PHNs learns the entire Pareto front in roughly the same time as learning a single point on the front, and also reaches a better solution set. PFL opens the door to new applications where models are selected based on preferences that are only available at run time.
