Data Free Learning of Reduced-Order Kinematics
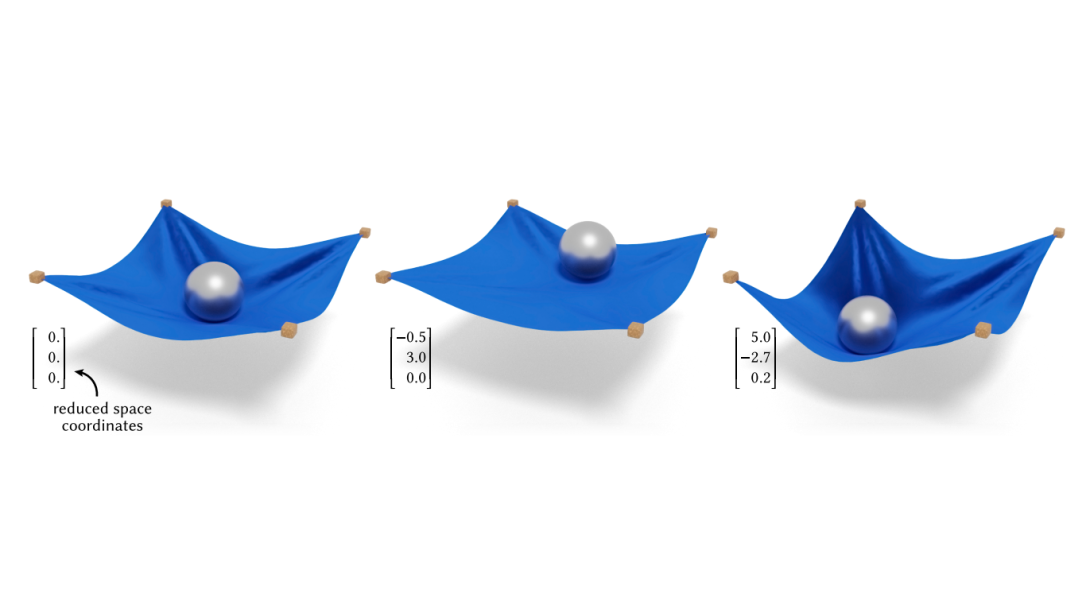
Physical systems ranging from elastic bodies to kinematic linkages are defined on a high-dimensional configuration spaces, yet their typical low-energy configurations are concentrated on much lower-dimensional subspaces. This work addresses the challenge of identifying such subspaces automatically: given as input an energy function for a high-dimensional system, we produce a low-dimensional map whose image parameterizes a diverse yet low-energy submanifold of configurations. The only additional input needed is a single seed configuration for the system to initialize our procedure; no dataset of trajectories is required. We represent subspaces as neural networks that map a low-dimensional latent vector to the full configuration space, and propose a training scheme to fit network parameters to any system of interest. This formulation is effective across a very general range of physical systems; our experiments demonstrate not only nonlinear and very low-dimensional elastic body and cloth subspaces, but also challenging systems like colliding rigid bodies and linkages, which resist conventional local analysis.We briefly explore applications built on this formulation, including manipulation, latent interpolation, and sampling.
