Graph Neural Networks for Enhanced Decoding of Quantum LDPC Codes
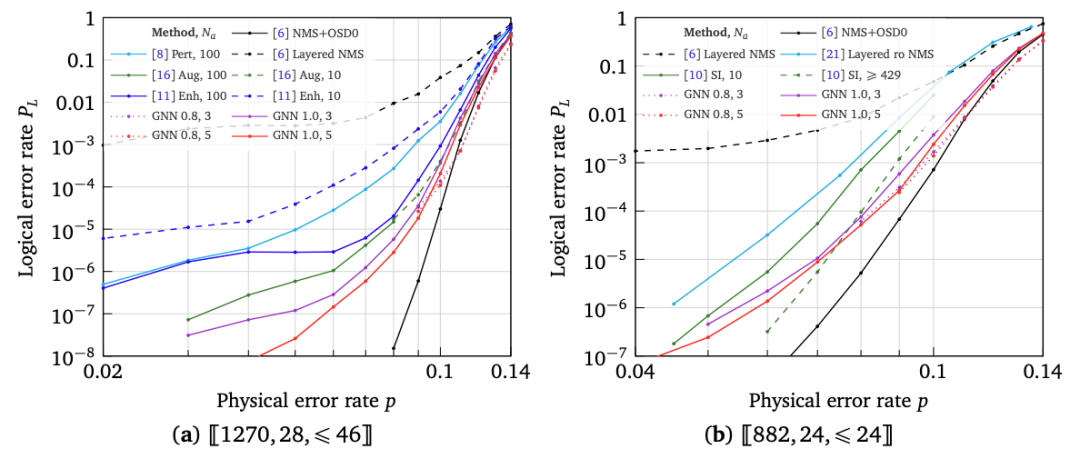
In this work, we propose a fully differentiable iterative decoder for quantum low-density parity-check (LDPC) codes. The proposed algorithm is composed of classical belief propagation (BP) decoding stages and intermediate graph neural network (GNN) layers. Both component decoders are defined over the same sparse decoding graph enabling a seamless integration and scalability to large codes. The core idea is to use the GNN component between consecutive BP runs, so that the knowledge from the previous BP run, if stuck in a local minima caused by trapping sets or short cycles in the decoding graph, can be leveraged to better initialize the next BP run. By doing so, the proposed decoder can learn to compensate for sub-optimal BP decoding graphs that result from the design constraints of quantum LDPC codes. Since the entire decoder remains differentiable, gradient descent-based training is possible. We compare the error rate performance of the proposed decoder against various post-processing methods such as random perturbation, enhanced feedback, augmentation, and ordered-statistics decoding (OSD) and show that a carefully designed training process lowers the error-floor significantly. As a result, our proposed decoder outperforms the former three methods using significantly fewer post-processing attempts. The source code of our experiments is available online.
