Graph Positional Encoding via Random Feature Propagation

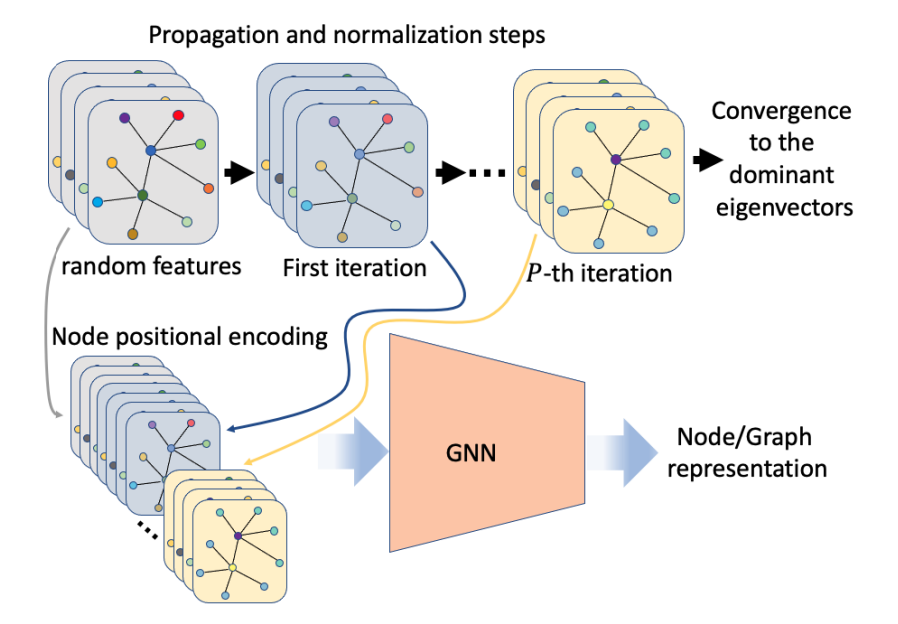
Two main families of node feature augmentation schemes have been explored for enhancing GNNs: random features and spectral positional encoding. Surprisingly, however, there is still no clear understanding of the relation between these two augmentation schemes. Here we propose a novel family of positional encoding schemes which draws a link between the above two approaches and improves over both. The new approach, named Random Feature Propagation (RFP), is inspired by the power iteration method and its generalizations. It concatenates several intermediate steps of an iterative algorithm for computing the dominant eigenvectors of a propagation matrix, starting from random node features. Notably, these propagation steps are based on graph-dependent propagation operators that can be either predefined or learned. We explore the theoretical and empirical benefits of RFP. First, we provide theoretical justifications for using random features, for incorporating early propagation steps, and for using multiple random initializations. Then, we empirically demonstrate that RFP significantly outperforms both spectral PE and random features in multiple node classification and graph classification benchmarks