MatBuilder: Mastering Sampling Uniformity Over Projections

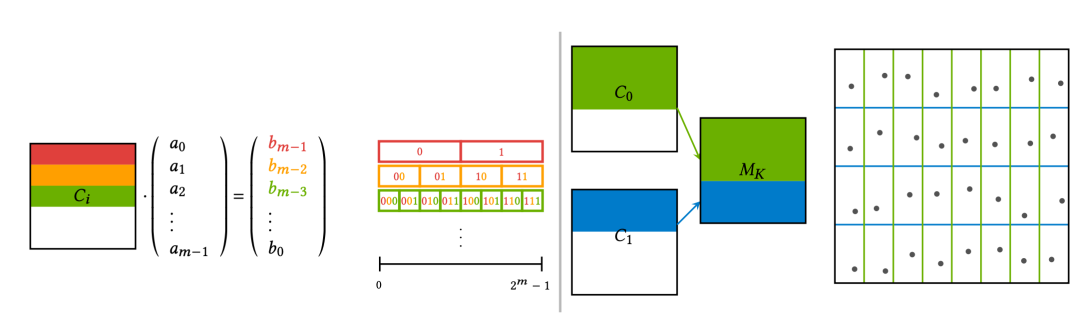
Many applications ranging from quasi-Monte Carlo integration over optimal control to neural networks benefit from high-dimensional, highly uniform samples. In the case of computer graphics,  and more particularly in rendering, despite the need for uniformity, several sub-problems expose a low-dimensional structure. In this context, mastering sampling uniformity over projections while preserving high-dimensional uniformity has been intrinsically challenging. This difficulty may explain the relatively small number of mathematical constructions for such samplers. We propose a novel approach by showing that uniformity constraints can be expressed as an integer linear program that results in a sampler with the desired properties. As it turns out, complex constraints are easy to describe by means of stratification and sequence properties of digital nets. Formalized using generator matrix determinants, our new MatBuilder software solves the set of constraints by iterating the linear integer program solver in a greedy fashion to compute a problem-specific set of generator matrices that can be used as a drop-in replacement in the popular digital net samplers. The samplers created by MatBuilder achieve the uniformity of classic low discrepancy sequences. More importantly, we demonstrate the benefit of the unprecedented versatility of our constraint approach with respect to low-dimensional problem structure for several applications.