As-Locally-Uniform-as-Possible Reshaping of Vector Clip Art

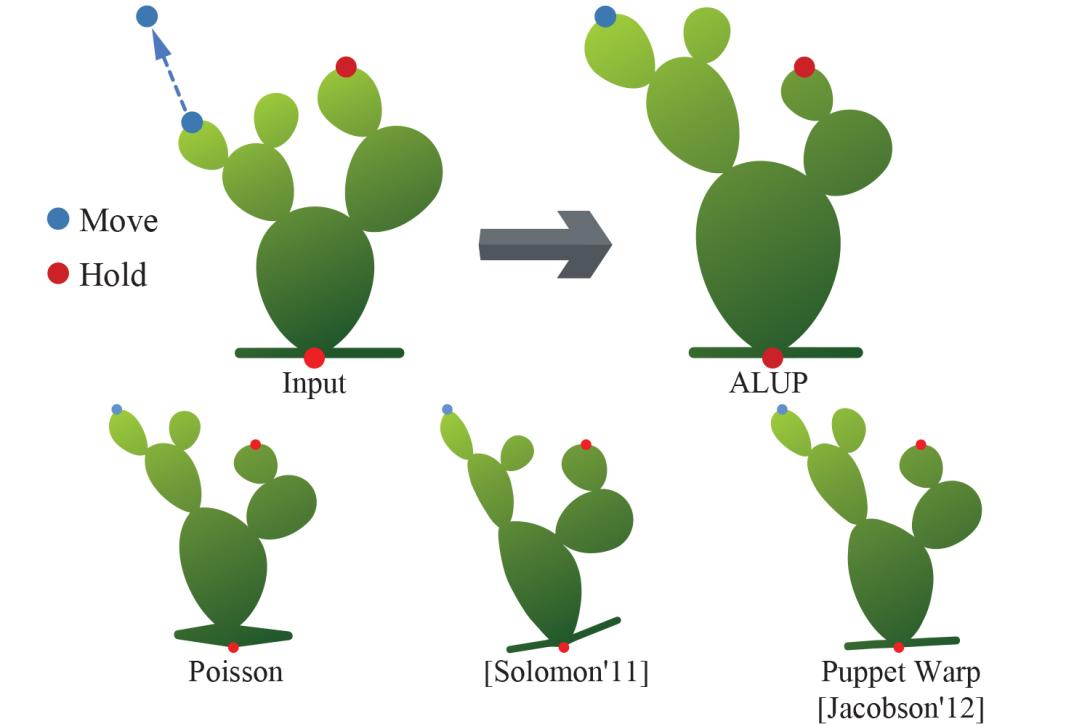
Vector clip-art images consist of regions bounded by a network of vector curves. Users often wish to reshape, or rescale, existing clip-art images by changing the locations, proportions, or scales of different image elements. When reshaping images depicting synthetic content they seek to preserve global and local structures. These structures are best preserved when the gradient of the mapping between the original and the reshaped curve networks is locally as close as possible to a uniform scale; mappings that satisfy this property maximally preserve the input curve orientations and minimally change the shape of the input's geometric details, while allowing changes in the relative scales of the different features. The expectation of approximate scale uniformity is local; while reshaping operations are typically expected to change the relative proportions of a subset of network regions, users expect the change to be minimal away from the directly impacted regions and expect such changes to be gradual and distributed as evenly as possible. Unfortunately, existing methods for editing 2D curve networks do not satisfy these criteria.



We propose a targeted As-Locally-Uniform-as-Possible (ALUP) vector clip-art reshaping method that satisfies the properties above. We formulate the computation of the desired output network as the solution of a constrained variational optimization problem. We effectively compute the desired solution by casting this continuous problem as a minimization of a non-linear discrete energy function, and obtain the desired minimizer by using a custom iterative solver.



We validate our method via perceptual studies comparing our results to those created via algorithmic alternatives and manually generated ones. Participants preferred our results over the closest alternative by a ratio of 6 to 1.