Phantom Ray-Hair Intersector

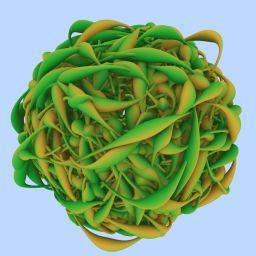
We present a new approach to ray tracing swept volumes along trajectories defined by cubic Bézier curves. It performs at two-thirds of the speed of ray-triangle intersection, allowing essentially even treatment of such primitives in ray tracing applications that require hair, fur, or yarn rendering. At each iteration, we approximate a radially symmetric swept volume with a tangential cone. A distance from the ray-cone intersection to the cone's base is then used to compute the next curve parameter t. When this distance is zero, the ray intersects the swept volume and the cone at the same point and we stop the iterations. To enforce continuity of the iterative root finding, we introduce "phantom" intersection, padding the cone until it touches the ray if the ray-cone intersection does not exist.